iA

L’intelligence artificielle moderne repose sur plusieurs concepts fondamentaux organisés en une hiérarchie allant du machine learning classique jusqu’aux modèles génératifs les plus avancés, comme les grands modèles de langage (LLM) et les modèles de diffusion utilisés pour générer des images ou des vidéos.
Cet article vous propose une cartographie claire et structurée de ces notions, afin de comprendre comment ces systèmes fonctionnent, comment ils s’organisent et comment ils produisent des résultats aussi impressionnants que ChatGPT, LLaMA, Stable Diffusion ou Midjourney.

Machine Learning : la base de l’apprentissage automatique

Le machine learning est une branche de l’intelligence artificielle qui permet aux machines d’apprendre à partir de données sans être explicitement programmées.
Il se divise en trois grandes familles.

Apprentissage supervisé

Le modèle apprend à partir d’exemples annotés, c’est-à-dire avec les bonnes réponses.

Exemples de tâches :

• Classification (ex : reconnaître un chat ou un chien)
• Régression (ex : prédire un prix ou une température)

Algorithmes courants :

• Régression linéaire
• K plus proches voisins
• Réseaux de neurones
• Arbres de décision

Apprentissage non supervisé

Le modèle découvre des structures et des patterns dans les données.

Exemples :

• Clustering
• Réduction de dimension (comme t-SNE, souvent utilisé pour visualiser des clusters)

Apprentissage par renforcement

Le modèle apprend par essais et erreurs, en recevant des récompenses.

Le Deep Learning : apprendre à grande échelle

Le deep learning repose sur des réseaux de neurones artificiels organisés en couches.
Plus les couches sont nombreuses, plus le modèle peut apprendre des structures complexes.

Réseau de neurones (ANN)

Un réseau de neurones est composé de nœuds (neurones) reliés entre eux par des poids. Chaque neurone transforme son entrée et transmet une information à la couche suivante.

Réseau de neurones multicouche (MLP)

C’est la version “profonde” du réseau de neurones.
On y trouve :

• des couches d’entrée
• plusieurs couches cachées
• une couche de sortie

Les MLP sont utilisés pour :

• la classification
• la régression
• la représentation de données

Rétropropagation du gradient

C’est la méthode d’apprentissage standard.
Le modèle ajuste progressivement ses poids pour réduire l’erreur entre sa prédiction et la bonne réponse.

Les architectures spécialisées du deep learning

Réseaux convolutifs (CNN)

Les CNN sont conçus pour analyser des images grâce à des filtres qui détectent des motifs (lignes, textures, formes).

Applications :

• classification d’images
• détection d’objets
• traitement vidéo

Réseaux récurrents (RNN, LSTM)

Ces réseaux traitent des données séquentielles comme :

• le texte
• l’audio
• les séries temporelles

Ils conservent une “mémoire” du passé, mais ont été largement remplacés par les transformeurs.

Les Transformeurs : la révolution de 2017

L’architecture des transformers est aujourd’hui au cœur des modèles les plus performants.
Elle repose sur le mécanisme d’attention, qui permet au modèle de comprendre quelles parties de l’entrée sont les plus importantes, quelles que soient leur position.

Avantages :

• traitement parallèle massif
• compréhension du contexte élargie
• adaptation au texte, à l’image, à la vidéo

Les transformeurs ont permis l’émergence :

• des LLM (GPT, LLaMA, Claude…)
• des modèles génératifs de texte
• des modèles de vision avancés
• des modèles text-to-image

Les modèles de langage (LLM)

Les grands modèles de langage sont construits sur l’architecture transformer.
Ils apprennent à prédire le mot suivant dans une séquence, après avoir été exposés à des trillions de tokens (morceaux de texte).

Fonctionnement général :

1. Tokenisation du texte
2. Transformation en vecteurs (embeddings)
3. Passage dans des dizaines à centaines de couches Transformer
4. Prédiction du prochain token
5. Génération de texte

Exemples de modèles :

• ChatGPT
• LLaMA
• Gemini
• Claude

Les modèles génératifs

Les modèles génératifs apprennent non seulement à analyser des données, mais aussi à créer de nouvelles données.

GAN (Generative Adversarial Networks)

Deux réseaux s’affrontent : l’un crée, l’autre critique.
Très efficaces pour générer des images réalistes.

Auto-encodeurs (VAE)

Ils apprennent à compresser puis reconstruire des données.

Modèles de diffusion

Aujourd’hui les plus utilisés pour la génération d’images.
Ils apprennent à transformer du bruit en image cohérente en plusieurs étapes.

Principe :

1. On ajoute du bruit à une image
2. Le modèle apprend à retirer ce bruit
3. Pendant la génération, le modèle part du bruit et “remonte” le processus

Exemples :

• Stable Diffusion
• Midjourney (basé sur diffusion + améliorations propriétaires)

Les systèmes multimodaux modernes

Les modèles actuels peuvent traiter et générer plusieurs types de données.
Voici les correspondances les plus courantes :

• Text-to-Text : ChatGPT, LLaMA
• Text-to-Image : Stable Diffusion
• Text-to-Video : Sora, Runway
• Vidéo-to-Text : analyse vidéo, sous-titres automatiques
• Image-to-Video : modèles vidéo conditionnés par image

Dans ces pipelines, chaque modalité possède :

• un encodeur adapté
• un modèle central (transformer ou diffusion)
• un décodeur propre à la sortie souhaitée

‍

Données et information

L’ère du Big Data

On estime qu'on produit autant de données que tout ce qui a été produit depuis le début de l'histoire de l'humanité jusqu'en 2003. Cette estimation est souvent attribuée à Eric Schmidt, ancien PDG de Google, qui l'a faite en 2010 lors d'une conférence à l'Université de Californie à Berkeley. On donne un terme à l’avènement de cette démesure : BIG DATA.

Enjeux de la représentation

La production et l’utilisation de plus en plus massive de ces données pose les enjeux de leur représentation. Qu’il soit question de capturer notre environnement, d’étudier leur structures, les réseaux, les systèmes ou encore d’identifier les relations au sein des données afin de mieux saisir la nature des interactions au sein d’un ensemble d’objets, la visualisation de ces grands ensembles constitue une discipline très utile connue sous le nom de datavisualisation.

Elle s’appuie sur un formalisme visuel au service du signifiant que l’on souhaite extraire de ces données, on parle alors de graphe, de diagramme, de réseaux, d'arbre, de nuage de points, de cartes…

L’analyse des réseaux relationnels en constitue une des applications concrète ; elle puise en partie ses inspirations dans la théorie des graphes, lesquels sont des modèles abstraits de dessins de réseaux reliant des objets. Ils peuvent comporter des nœuds, des sommets, des arêtes, des courbes, des polygones, des couleurs, des légendes.

Une abstraction de la réalité

Il paraît dérisoire de penser qu’une simple représentation puisse se saisir de toute la complexité d’un phénomène : il s’agirait plutôt d’une abstraction de la réalité. Une certaine forme de sens émerge néanmoins. On discerne des tendances, des motifs.

La possibilité d’interagir directement avec une visualisation apporte un éclairage sur le caractère versatile des données. La représentation est avant tout une affaire de point de vue.

Dataviz

Un outil fondamental

Dans le contexte actuel de l’expansion des systèmes de données, la visualisation de données se révèle être un outil fondamental dans le traitement de l’information par l’Homme, de surcroît lorsqu'il s'agit de mettre en relation les différentes variables d’un phénomène.

Entre idée et forme

La recherche de nouvelles formes de visualisation met en évidence le lien profond entre une idée et sa représentation graphique, dans le but d'imager des concepts parfois difficiles à appréhender. Cela se traduit par un ensemble dans lequel les données ne sont qu’autant d'éléments d'un tout, qui, ensemble, constituent un réseau tangible, un mouvement, une forme remarquable — l’émergence d'un ordre à travers le chaos de l’information.

De la classification du vivant

Arbres phylogénétiques

Comment classer et comprendre les milliers, voire les millions d'organismes différents qui peuplent notre planète ? Dans les premiers temps, les naturalistes se fondaient principalement sur l'observation des caractéristiques physiques des organismes pour les classer. Cependant, cette approche était sujette à des erreurs et ne reflétait pas toujours les véritables relations évolutives entre les espèces.

La révolution génétique

C'est avec l'avènement des technologies modernes que la classification des espèces a pris un tournant révolutionnaire. Les avancées dans le séquençage de l'ADN ont ouvert de nouvelles portes. En séquençant l'ADN de différentes espèces, les scientifiques ont pu accéder à une mine d'informations génétiques précieuses, révélant les liens souvent cachés entre les organismes.

Aujourd'hui, grâce aux techniques d'analyse génétique et de bio-informatique, nous sommes en mesure de reconstruire l'arbre de la vie avec une précision et une résolution sans précédent. La classification devient une exploration profonde de l'histoire génétique et évolutive des espèces.

Alignement des séquences

Principes et méthodes

Il existe plusieurs techniques de construction des arbres phylogénétiques, plus ou moins rapides et plus ou moins fiables. On peut optimiser plusieurs critères : la distance, la parcimonie, ou la vraisemblance. Pour les méthodes de distance, on choisit un critère de distance entre les feuilles (par exemple le nombre de nucléotides différents entre deux séquences).

Pour déterminer cette valeur, on effectue un alignement puis on peut utiliser la méthode UPGMA ou le Neighbour Joining pour déduire l'arbre.

Alignement des séquences

Il existe plusieurs techniques de construction des arbres phylogénétiques, plus ou moins rapides et plus ou moins fiables. On peut être amené à chercher à optimiser plusieurs critères dans l'arbre : la distance, la parcimonie, ou la vraisemblance.Pour les méthodes de distance, il s'agit tout d'abord de choisir le critère de distance entre les futures feuilles de l'arbre. Par exemple, si ces feuilles sont des séquences d'ADN, on peut choisir comme distance entre deux d'entre elles le nombre de nucléotides qui diffèrent. Pour déterminer cette valeur, on est amené à en effectuer un alignement. Puis on peut utiliser la méthode UPGMA ou celle du Neighbour joining pour en déduire l'arbre.

Sélection des séquences à aligner

Les séquences à aligner sont sélectionnées. Ces séquences peuvent provenir de différentes espèces, de différentes régions génomiques ou de différentes molécules biologiques (ADN, ARN, protéines).

Identification des régions similaires

Les algorithmes d'alignement recherchent des régions similaires entre les séquences. Ces régions peuvent être des séquences conservées, c'est-à-dire des parties de séquences qui sont présentes dans toutes les espèces étudiées et qui ont été conservées au cours de l'évolution en raison de leur importance fonctionnelle.

Construction de l'alignement

Une fois les régions similaires identifiées, l'algorithme construit un alignement en alignant les bases ou les acides aminés correspondants les uns en face des autres. L'objectif est de maximiser le nombre de correspondances (identités) entre les bases ou les acides aminés, tout en minimisant le nombre d'insertions et de suppressions nécessaires pour aligner les séquences.

Interprétation

Les résultats servent à tirer des conclusions sur les relations évolutives, identifier des régions fonctionnelles et prédire structures et fonctions protéiques.

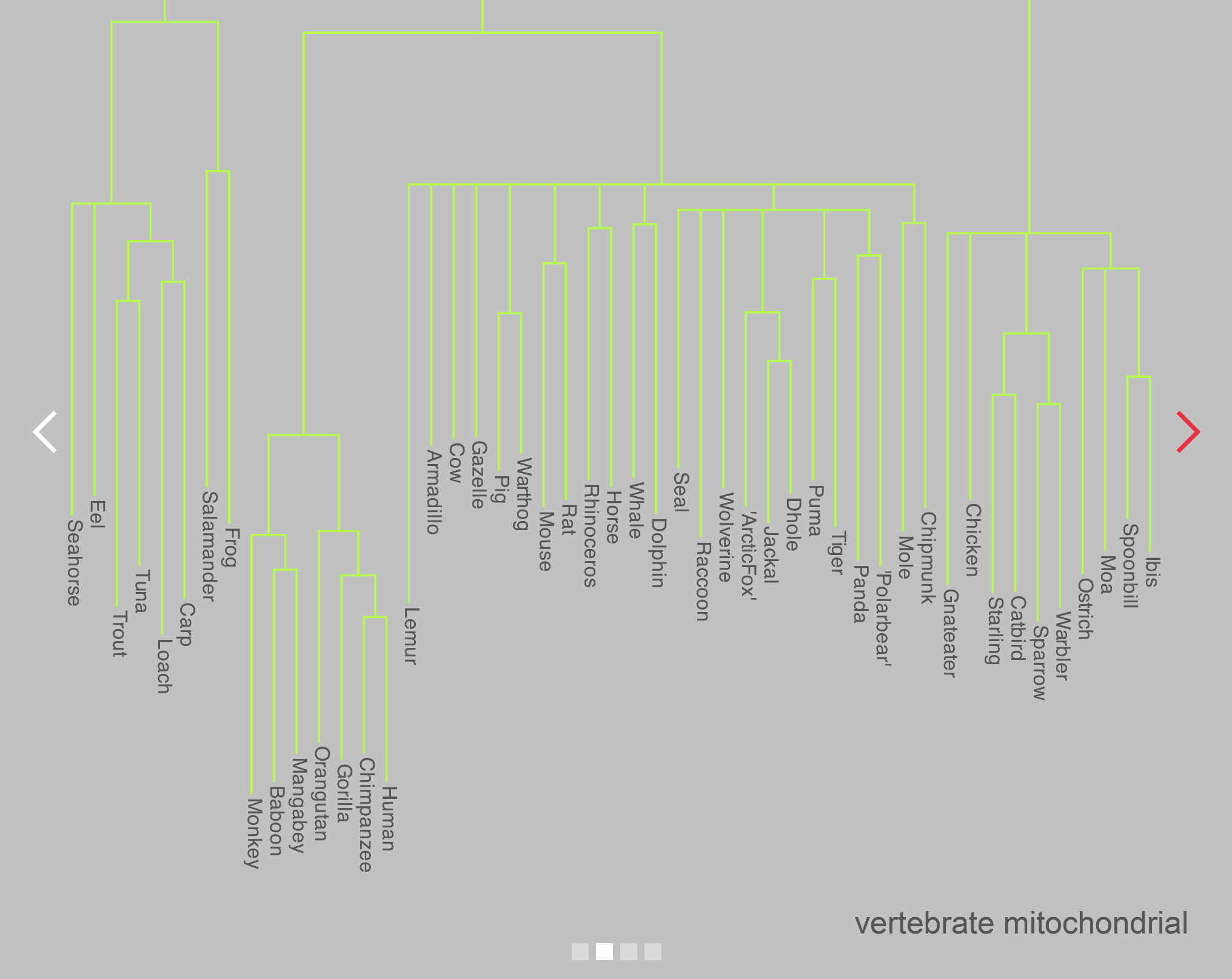
Base de données

NCBI Taxonomy

Le NCBI propose une base de données NCBI Taxonomy indicative. La taxonomie du NCBI représente environ 10 % des espèces vivantes de la planète. Elle sert de nomenclature organisée pour les séquences dans des bases publiques.

Le TaxID relie les trois bases de l'International Nucleotide Sequence Database Collaboration (INSDC) : DDBJ (Japan), NCBI (États-Unis) et EMBL-EBI (Europe).

Des systèmes

Définition et portée

Au sens philosophique : ensemble des principes qui servent de guide à l'interprétation de la réalité et à l'action.

En sciences : concept décrivant un phénomène complexe impliquant plusieurs composantes (espace, temps, mouvement, énergie) et leurs interactions.

“L’avenir à chaque instant presse le présent d’être un souvenir.” — Louis Aragon

Le mouvement

Platon, Aristote et d'autres ont réfléchi au mouvement : Platon listait des mouvements, Aristote liait mouvement et changement (puissance/acte), Zénon a posé des paradoxes sur la divisibilité de l'espace et du temps.

Une pierre qui tombe illustre la distinction entre être en puissance et être en acte.

La continuité et le temps

Le mouvement

Platon, Aristote et d'autres ont réfléchi au mouvement : Platon listait des mouvements, Aristote liait mouvement et changement (puissance/acte), Zénon a posé des paradoxes sur la divisibilité de l'espace et du temps. Une pierre qui tombe illustre la distinction entre être en puissance et être en acte.

Platon a donné sa liste des mouvements. Dans les Lois X, il mentionne dix mouvements : la rotation sur place dont celle des astres fixes, la translation sur un axe unique ou sur plusieurs emplacements comme celle des planètes, la combinaison, la séparation, l'accroissement, le décroissement, la génération, la destruction, les mouvements de l'âme et le mouvement du monde.

Dans le Timée, il détaille « six mouvements », ou plutôt directions : « en avant et en arrière », « vers le haut et vers le bas », « à droite et à gauche ».
Dans l'esprit d'Aristote, le mouvement et le changement sont étroitement liés. Il constate aussi que, bien que le mouvement (kinésis) soit plus facilement observable, ce qui compte, ce n'est pas le mouvement mais le changement (métabolé).

« Une pierre qui tombe n’est pas une pierre au sens strict, mais une pierre en puissance – elle peut devenir pierre. Ainsi, dans sa chute, elle se réalise à mesure qu’elle s’approche du sol, son lieu naturel. Une fois celui-ci atteint, la pierre est pierre en acte. »
— Sébastien Viscardy

Énergie potentielle ? (ndlr)

Cette affirmation contient les prémisses de l’idée de causalité : le mouvement limité de chaque chose s'inscrit d'une manière précise entre un état initial et un état final.

Le temps et le changement

Selon certaines conceptions philosophiques, le temps est étroitement lié au changement, de sorte qu'il ne pourrait exister en dehors de celui-ci.
Selon d'autres conceptions, le temps est considéré comme une entité indépendante du changement, qui existe en dehors de l’influence phénoménologique de l'univers physique.

La continuité du mouvement sur le plan métaphysique

« L'être n'est en devenir que relativement à l'être en acte. »
— Aristote

Zénon, dans ses paradoxes, avait mis au jour la dualité entre le mouvement fini et le temps infini du parcours.
La première intuition du mouvement est celle d’une transition spatiale, continue, entre deux points de l’espace séparés par d’infinies positions intermédiaires.
De manière analogue à la suite infinie des divisions entières, l’espace semble selon cette description être un continuum infini.
Pourtant, les mouvements perçus par nos sens s’effectuent bel et bien en un temps fini.

Selon Zénon, pour se déplacer d'un point A à un point B, il faut passer par une infinité de points intermédiaires, ce qui implique un mouvement continu et, par conséquent, demande un temps infini.
Ce paradoxe défie notre perception du mouvement et entre en conflit avec notre expérience quotidienne.

« L’avenir n’est pas encore. Son infinité est en puissance, et non pas en acte. »
— Emmanuel Kant

La discrétisation du mouvement

La solution la plus courante consiste à considérer que la notion de mouvement continu est une abstraction mathématique, et que dans la réalité, le mouvement est discontinu — c'est-à-dire qu'il se produit par sauts discrets d'un point à un autre.
Ainsi, on peut expliquer comment Achille peut rattraper la tortue en un temps fini, sans avoir à parcourir un nombre infini de distances intermédiaires.

L’introduction du concept d’état dynamique fournit une solution au paradoxe de Zénon.
L’état dynamique d’un système est un état instantané, mais c’est un état de mouvement.
Il est déterminé par les valeurs de toutes les variables d’état à cet instant.
L’état dynamique est un instantané de la configuration d’un système à un instant t.
C’est l’utilisation des équations différentielles qui permettra de décrire le mouvement.

Les équations du mouvement

Dans le cadre de la physique classique, le temps est généralement considéré comme une dimension continue et linéaire, s’écoulant sans interruption.
Cela signifie que le temps peut être divisé en un nombre infini de parties, chacune étant plus petite que la précédente, mais sans limite inférieure.
Dans cette perspective, le temps est considéré comme un continuum.

La question de savoir si le temps est continu ou discret a été débattue par les philosophes, les mathématiciens et les physiciens pendant des siècles.

La continuité topologique en mathématiques

L’analogie mathématique qui découle de la réflexion sur la notion de continuité au sein de l’ensemble des nombres réels fonda les bases du calcul infinitésimal en proposant les outils mathématiques connus sous le nom de calcul différentiel, de calcul intégral ou encore de calcul des variations, s’inscrivant aujourd’hui dans le cadre de l’analyse réelle — la branche de l’analyse qui étudie les ensembles de réels et les fonctions de variables réelles.

Fort de ces outils mathématiques, on considère dans les équations du mouvement que la vitesse est la dérivée de l’accélération par rapport au temps.

La continuité temporelle en physique

Il est souvent considéré que l'espace de Planck, qui est l'échelle de longueur la plus petite possible selon la physique actuelle, peut être interprété comme une grille de cellules d'espace.
Cette grille est souvent appelée grille de Planck ou structure discrète de l'espace-temps.

Selon la théorie de la relativité générale d'Einstein, l'espace-temps est une entité dynamique qui peut être courbée par la présence de matière et d'énergie.
Cependant, dans certaines théories de la physique quantique, il est également suggéré que l'espace-temps pourrait avoir une structure quantique discrète à des échelles très petites.

Dans cette perspective, l'espace de Planck peut être considéré comme une grille de cellules d'espace, où chaque cellule a une taille de l'ordre de la longueur de Planck (environ 10⁻³⁵ m).
Cette grille de Planck pourrait avoir des propriétés particulières, telles que la quantification de l'espace et la limitation de la précision avec laquelle nous pouvons mesurer les distances.

Le temps de Planck est la plus petite unité de temps qui ait un sens physique dans notre univers.
Il est dérivé à partir de la constante de Planck, une constante fondamentale de la physique quantique.
En d'autres termes, si le temps est discrétisé à des échelles très petites, il se pourrait que les événements ne puissent pas se produire en dessous d'une certaine échelle de temps — et cette échelle serait le temps de Planck.

‍

‍

Dynamique des systèmes

Un système dynamique décrit l’évolution d’un système en fonction du temps.
Les composantes qui caractérisent ce système sont des variables d’état, représentées par une fonction d’état qui décrit sa progression.

L'étude des systèmes dynamiques vise à décrire les changements dans le temps et l'espace — les transformations — de l'état des systèmes, en fonction des causes de ces changements, dans la mesure où ces causes sont les interactions internes entre les objets du système.

L’idée de système fournit un cadre d’analyse pour l’étude des phénomènes physiques, ainsi que des outils d’abstraction mathématique permettant de les étudier.

Lorsque l'évolution des systèmes dynamiques peut être modélisée par des systèmes d'équations différentielles ordinaires, le comportement de chaque variable du système est défini par sa tendance à tout moment — augmenter, diminuer, rester stable — en fonction de l'influence des autres variables.
On résout mathématiquement un système dynamique si l'on peut retracer l'évolution de chaque variable en fonction du temps, c’est-à-dire intégrer les équations différentielles.

Systèmes dynamiques à temps discrets

Un système dynamique à temps discret est un système dont l’évolution est décrite par étapes, c’est-à-dire en un nombre fini d’instants.
Les variables du système sont réactualisées à intervalles réguliers, à la manière d’un métronome, ou du moins à des moments précis dans le temps, plutôt qu’en continu.

Ces systèmes peuvent être exprimés par des équations de récurrence (ou boucles), qui décrivent l’évolution des variables du système d'une étape à la suivante, en fonction de leur état actuel et des entrées.
Une analogie existe entre la récurrence d'une équation et la boucle for en programmation informatique : la récurrence permet de définir une suite de valeurs qui évolue à chaque itération.

Le principe de moindre action

« Lorsqu’il arrive quelque changement dans la nature, la quantité d’action nécessaire pour ce changement est la plus petite qui soit possible. »
— Pierre-Louis Moreau de Maupertuis

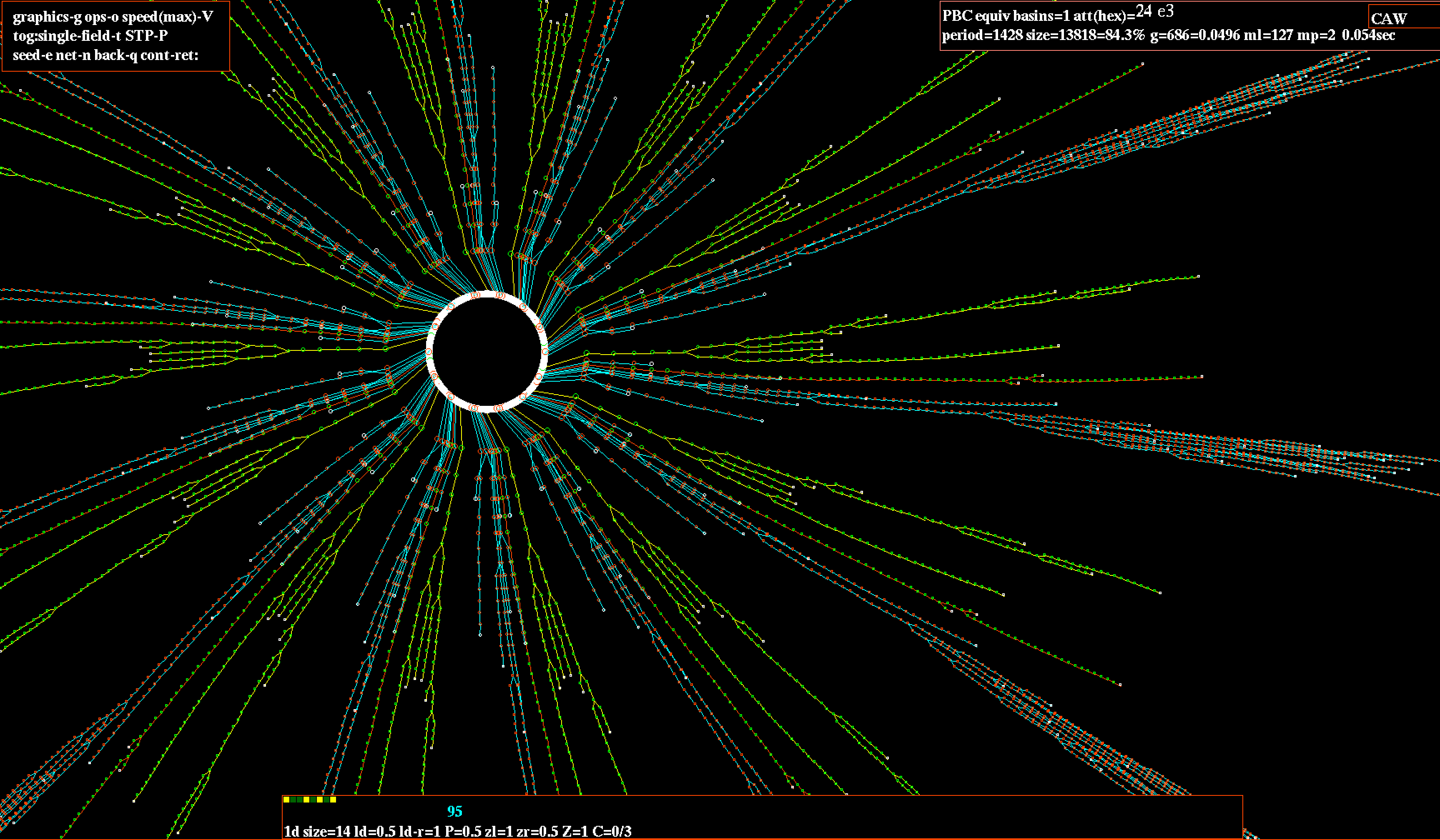
Les systèmes dynamiques à temps discret sont utilisés dans de nombreux domaines de la science et de l'ingénierie : biologie, physique, finance, ou encore intelligence artificielle.
Ils servent notamment à modéliser des systèmes de contrôle, des réseaux de neurones, ou encore des systèmes de traitement du signal.

Systèmes non linéaires et chaos

Sensibilité aux conditions initiales

La sensibilité aux conditions initiales est un phénomène découvert à la fin du XIXe siècle par Henri Poincaré, dans le cadre du problème des N corps en mécanique céleste.
Cette sensibilité explique que, pour un système chaotique, des modifications infimes des conditions initiales puissent entraîner des résultats radicalement différents à long terme, rendant le phénomène imprévisible en pratique.
Ce résultat est souvent vulgarisé sous le nom d’effet papillon.

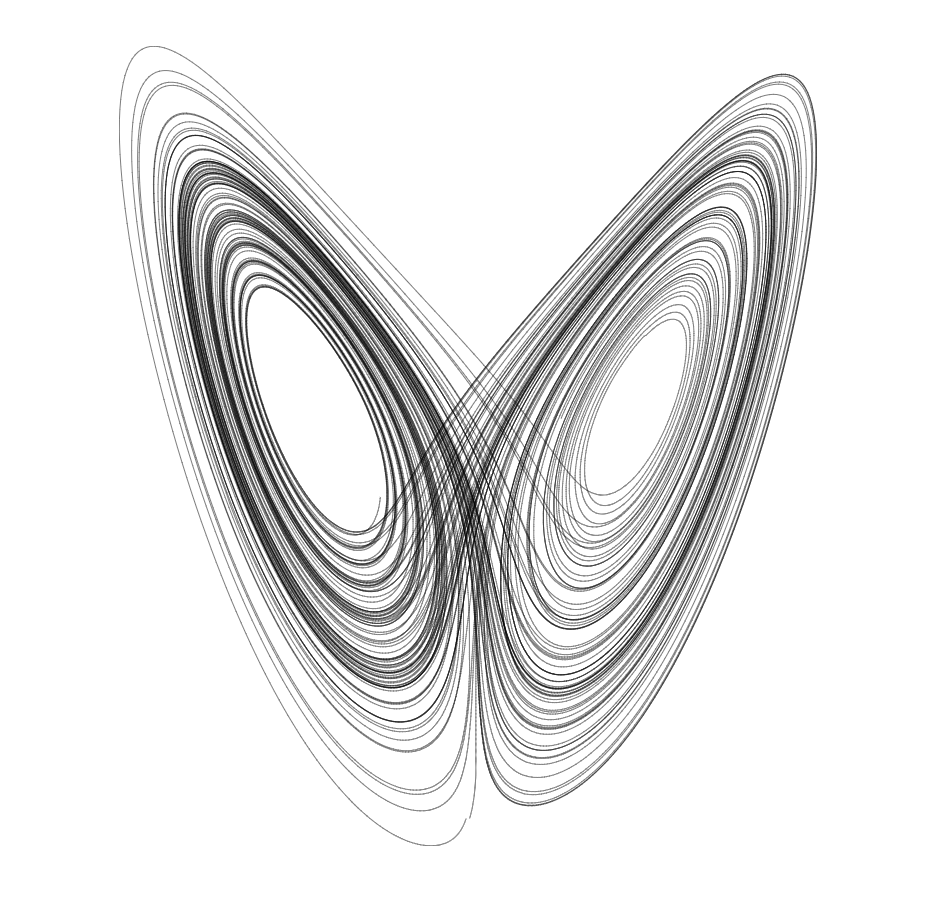
L’attracteur de Lorenz — Chaos et harmonie

D’un point de vue déterministe, une connaissance parfaite des conditions initiales d’un système chaotique devrait théoriquement le rendre prévisible.
Cependant, la nature intrinsèquement complexe de ces systèmes rend leur comportement souvent imprévisible à long terme, même lorsque les conditions initiales sont connues avec précision.

Contrairement à un simple pendule, dont le mouvement est régulier et prévisible, le double pendule est un système non linéaire : il est plus complexe et difficile à anticiper.
De petites variations dans l’angle ou la vitesse initiale peuvent produire des trajectoires très différentes.

Ce comportement chaotique découle de la dynamique non linéaire et de la sensibilité aux conditions initiales.
Ainsi, bien que ces systèmes soient déterministes — régis par des lois précises — ils produisent des comportements qui semblent aléatoires et imprévisibles.

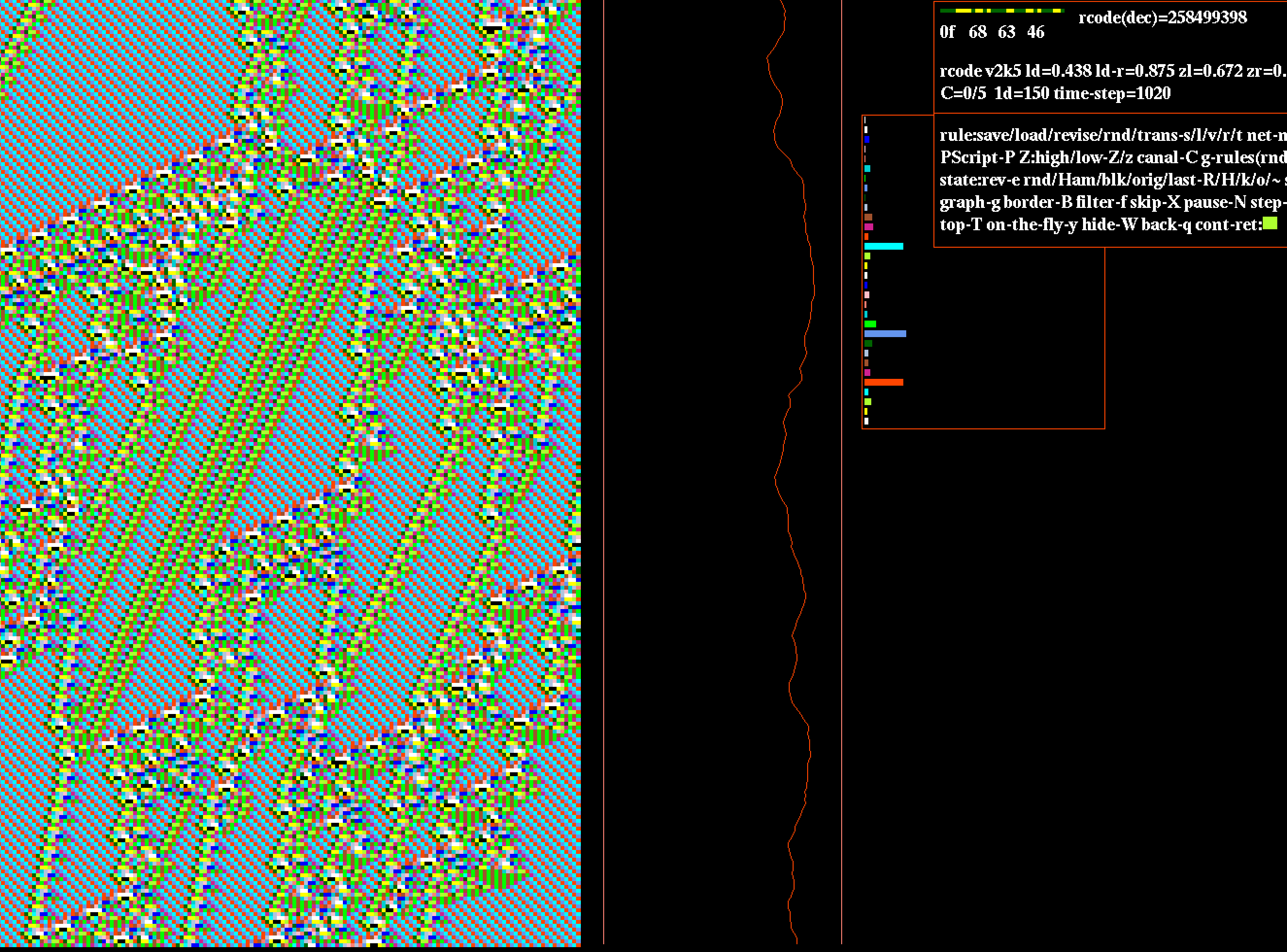
Automates cellulaires et systèmes dynamiques

Un automate cellulaire est un modèle mathématique composé d'un ensemble de cellules disposées dans un réseau régulier, comme une grille ou un réseau hexagonal.
Chaque cellule peut prendre un nombre fini d'états distincts, et son état évolue selon un ensemble de règles locales dépendant de ses voisines.

Simulation de phénomènes

Les automates cellulaires peuvent être utilisés pour modéliser une grande variété de phénomènes dans des domaines tels que la biologie, la physique, la chimie, la sociologie ou l'économie.
Ils peuvent par exemple représenter :

• la croissance de colonies bactériennes,
• la propagation d’un feu de forêt,
• ou la dynamique des fluides.

Complexité et émergence

À partir de règles simples et locales, les automates cellulaires génèrent des comportements complexes et imprévisibles.
Ils permettent d’étudier comment des structures globales émergent d’interactions locales — un principe fondamental de l’auto-organisation.

En explorant différentes configurations initiales et règles de transition, on observe comment les motifs évoluent dans le temps, donnant naissance à des structures stables, périodiques ou chaotiques.

Le Jeu de la vie

Le Jeu de la vie de John Conway est l’un des automates cellulaires les plus célèbres.
Il se déroule sur une grille bidimensionnelle de cellules, chaque cellule étant soit vivante (active) soit morte (inactive).

Les règles sont simples :

• une cellule vivante survit si elle a deux ou trois voisins vivants ;
• sinon, elle meurt par sous-population ou surpopulation ;
• une cellule morte devient vivante si elle a exactement trois voisins vivants.

Ce jeu a suscité des discussions philosophiques sur la vie, l’intelligence artificielle et la complexité de l’univers.
Il montre comment des règles simples peuvent engendrer des dynamiques émergentes fascinantes, posant des questions profondes sur la nature du calcul et de la réalité.

Le Glider

Un glider est un motif caractéristique dans les automates cellulaires bidimensionnels, notamment dans le Jeu de la vie.
C’est une configuration mobile de cellules qui se déplace à travers la grille tout en conservant sa forme.

Dans le Jeu de la vie, un glider se déplace diagonalement, à une vitesse de un pas tous les quatre cycles.
Autrement dit, après quatre étapes, il se retrouve décalé d’une cellule vers le bas et d’une cellule vers la droite (ou la gauche, selon l’orientation).

Les gliders sont fascinants car ils incarnent une structure mobile stable dans un système régi par des lois statiques.
Ils illustrent comment, à partir de règles élémentaires, le mouvement, la communication et la complexité peuvent émerger spontanément.

‍

Émergence et morphogenèse

L'émergence

Le phénomène d’émergence se manifeste quand des motifs ou comportements complexes apparaissent de l'interaction entre composants d'un système.

Morphogenèse

Alan Turing (1952) montra comment des réactions et diffusions chimiques (morphogènes) peuvent créer des motifs auto-organisés, expliquant des motifs naturels (taches, bandes) et contribuant à la compréhension du développement biologique.

Quand l'esprit humain, avec son pouvoir limité...

« Quand l'esprit humain, avec son pouvoir limité, tente de reproduire en lui-même la riche vie du monde, dont il est lui-même une petite partie, et dont il ne peut jamais espérer s'extraire, il a toutes les raisons de procéder économiquement. »

Particle physics

La métaphore du cylindre est l'exemple d'un objet ayant des propriétés apparemment inconciliables.
Il serait à première vue déroutant d'affirmer qu'un objet ait à la fois les propriétés d'un disque et d'un rectangle : sur un plan, un objet est soit un disque, soit un rectangle.
Mais si l'on considère un cylindre : une projection suivant l'axe du cylindre donne un disque, et une projection perpendiculairement à cet axe donne un rectangle.

Dualité onde-corpuscule

La perception prête aux erreurs d’interprétation et nous conduit souvent à ne faire qu'effleurer la surface des choses.
Cela a conduit certains philosophes à postuler l’idée que la connaissance se devait d’être un travail unique de la pensée.

Galilée avait bien compris que la perception du monde à travers le prisme des sens nous expose à une représentation incomplète, voire biaisée, du monde qui nous entoure — interdisant tout raisonnement élaboré à partir d’une observation directe.

L'illusion des perceptions

Le philosophe et poète latin Lucrèce (60 av. J.-C.) donne une remarquable description du mouvement des particules selon les principes d'Épicure dans son œuvre De la nature :

"Si tu penses que les atomes, principes des choses, peuvent trouver le repos et dans ce repos engendrer toujours de nouveaux mouvements, tu te trompes et t'égares loin de la vérité. [...]
Puisqu'il en est ainsi, il ne peut y avoir aucun repos pour les atomes à travers le vide immense; au contraire, agités d'un mouvement continuel et divers, ils se heurtent, puis rebondissent, les uns à de grandes distances, les autres faiblement, et s'éloignent peu."
— Lucrèce, De rerum natura

L'expérience de pensée

« Supposons que nous puissions attribuer à la nature la propriété de produire des évènements semblables dans des circonstances semblables; nous ne saurions simplement pas comment trouver ces circonstances semblables. La nature est unique. Ces évènements semblables sont une production de notre schéma mental. »

L'unique puissance de l'imagination humaine

« L'objectif que [la physique] s'est fixé est l'expression abstraite la plus simple et la plus économique des faits. »

En se libérant de toute contrainte liée au monde physique, on peut dès lors imaginer l’irréalisable.
C’est une erreur de penser que la pensée analytique condamne l’expérimentation : Galilée lui-même s’est appuyé sur des expériences de pensée.

Sa démonstration, selon laquelle la vitesse de chute d’un corps ne dépend pas de sa masse, repose sur un raisonnement logique pur, lui permettant de contredire Aristote.

C’est également ce qui permit à Démocrite, dans un extraordinaire élan d’intuitivité, de postuler l’existence d’un monde fait d’atomes.
Considéré comme le fondateur de la pensée atomiste, il proposa avec Leucippe une vision révolutionnaire du monde.
Reprise plus tard par Lucrèce dans De rerum natura, cette conception anticipait déjà l’idée moderne que la matière tire ses propriétés de l’organisation de ses constituants fondamentaux.

« Un problème de minimum qui consiste à exposer les faits aussi parfaitement que possible avec la moindre dépense intellectuelle. »

Les concepts évoqués ici sont d’une remarquable justesse, et pourtant formulés il y a plus de 2000 ans.
La pensée de Démocrite illustre deux idées fondatrices :

• la matière tire sa diversité de l’organisation interne de ses sous-constituants ;
• il existe une unité insécable — l’atome —, représentation contre-intuitive mais profondément juste du monde physique.

‍

‍

La validation des théories par la mesure

« Les savants doivent utiliser les concepts les plus simples pour parvenir à leurs résultats et exclure tout ce qui ne peut être perçu par les sens. »

La physique théorique et la physique expérimentale sont complémentaires.
La vérification expérimentale d’une prédiction théorique est une étape décisive qui permet de valider une hypothèse avec plus ou moins de certitude.
L’expérience n’établit pas de vérité absolue, mais elle confirme une observation ou appuie une hypothèse issue d’une prédiction.

La physique expérimentale s’attache à percevoir la réalité par l’expérience, tandis que la physique théorique tente de l’expliquer.
Une expérimentation s’applique à confirmer ou infirmer une théorie fondée sur la prédiction d’un phénomène, tout en affinant la connaissance des constantes physiques.

« Quand, par la pensée, nous séparons un objet de l'environnement mouvant dans lequel il évolue, ce que nous faisons en réalité est extirper un ensemble de sensations [...] possédant une stabilité relativement plus élevée que les autres. »

Sonder la matière

Le CERN (Organisation européenne pour la recherche nucléaire) est l'un des plus grands laboratoires de recherche en physique des particules au monde.
Il abrite notamment le LHC (Large Hadron Collider), le plus grand accélérateur de particules jamais construit. Des données sont mises à disposition via CERN Open Data.

Les chercheurs du CERN utilisent des détecteurs tels que le CMS (Compact Muon Solenoid) pour étudier les collisions de particules à des énergies extrêmes.
Ces expériences permettent de sonder la structure fondamentale de la matière et de mieux comprendre les lois de l’univers.

Les données recueillies lors de ces collisions sont mises à disposition du public via le projet CERN Open Data, permettant à la communauté scientifique et au grand public de participer à la découverte de nouvelles connaissances.

Le LHC — ou Grand collisionneur de hadrons — est un tunnel circulaire de près de 30 km de diamètre, équipé d’immenses détecteurs.
Il regroupe plusieurs expériences majeures : LHCb, ATLAS, CMS et ALICE.
Les particules chargées y sont accélérées à des vitesses proches de celle de la lumière afin d’étudier les produits de leurs collisions, repoussant les limites de notre compréhension du réel.

« En réalité, une loi contient moins que le fait lui-même, parce qu'elle ne reproduit pas le fait dans son ensemble mais seulement dans son aspect qui est le plus important à nos yeux, le reste étant ignoré intentionnellement ou par nécessité. »